DMTet

· May 21, 2023

Why DMTet

DMTet[1] is a hybrid explicit+implicit representation of a 3D geometry. On the explicit side, the object surface is in a tetrahedral-grid representation, and could be turned into mesh using Marching Tetrahedra (similar to Marching Cubes); then on the implicit side, the vertices in the tetrahedral-grid stores SDF values, and both the SDF values and the vertice positions are optimized by a neural network.

A lot of recent 3D generative methods[2, 3] decides to use DMTet in their pipelines because of its elusiveness and effectiveness. Now let’s take a closer look at the details.

Pipeline

Overview

Inputs: point clouds / coarse voxel

Outputs: fine mesh

The geometry generating pipeline follows a coarse-to-fine process.

Coarse Stage

Initialization

Initialize a coarse tetrahedral-grid for the input point cloud / voxel, then predict the SDF values of each vertice using neural network.

First a encoder is used to extract a feature volume $F_{\text {vol }}(x)$, then the volume could be used to interpolate a feature vector for each grid vertex, i.e. $F_{\text {vol }}(v, x)$.

Then, a MLP is used to predict the SDF values of the vertices:

\[(s(v), f(v))=\operatorname{MLP}\left(F_{\text {vol }}(v, x), v\right)\]

Fine Stage

In this stage, the surface and the tetrahedral grid are iteratively updated.

A graph $G = (V_{surf}, E_{surf})$ is built upon the tetrahedral grid, where $V_{surf}, E_{surf}$ are the vertices and edges in the grid, respectively. There are several steps in the refinement loop:

Surface Refinement

A SDF value and vertex position offset are calculated using a GCN, namely:

\[\left(\Delta v_i, \Delta s\left(v_i\right), \overline{f\left(v_i\right)}\right)_{i=1, \cdots N_{\text {surf }}} =\operatorname{GCN}\left(\left(f_{v_i}^{\prime}\right)_{i=1, \cdots N_{s u r f}}, G\right)\]

In which the feature $f_{v_i}^{\prime}$ is a concatenated feature from the encoder feature $F_{\text {vol }}\left(v_i, x\right)$ and MLP feature $f(v_i)$ from the initilization.

\[f_{v_i}^{\prime} =\operatorname{concat}\left(v_i, s\left(v_i\right), F_{\text {vol }}\left(v_i, x\right), f\left(v_i\right)\right)\]

After this step, the vertex position and the SDF value for vertex $v_i$ are updated as $v_i^{\prime}=v_i+\Delta v_i$ and $s\left(v_i^{\prime}\right)=$ $s\left(v_i\right)+\Delta s\left(v_i\right)$.

Volume Subdivision

The tetrahedral grid is defined as $(V_T, T)$, where $V_T$ are the vertices in the tetrahedral grid $T$. Each tetrahedron $T_k \in T$ has 4 vertices ${v_{ak}, v_{bk}, v_{ck}, v_{dk}}$. The subdivision after surface refinement goes like this:

1. Re-identify $T_{surf}$ from the new SDF values. A tetrahedron is viewed as being on surface when it has vertices with different SDF signs. Drop those without different signs.

2. Subdevide $T_{surf}$ . The subdivision process could be seen in this figure:

   

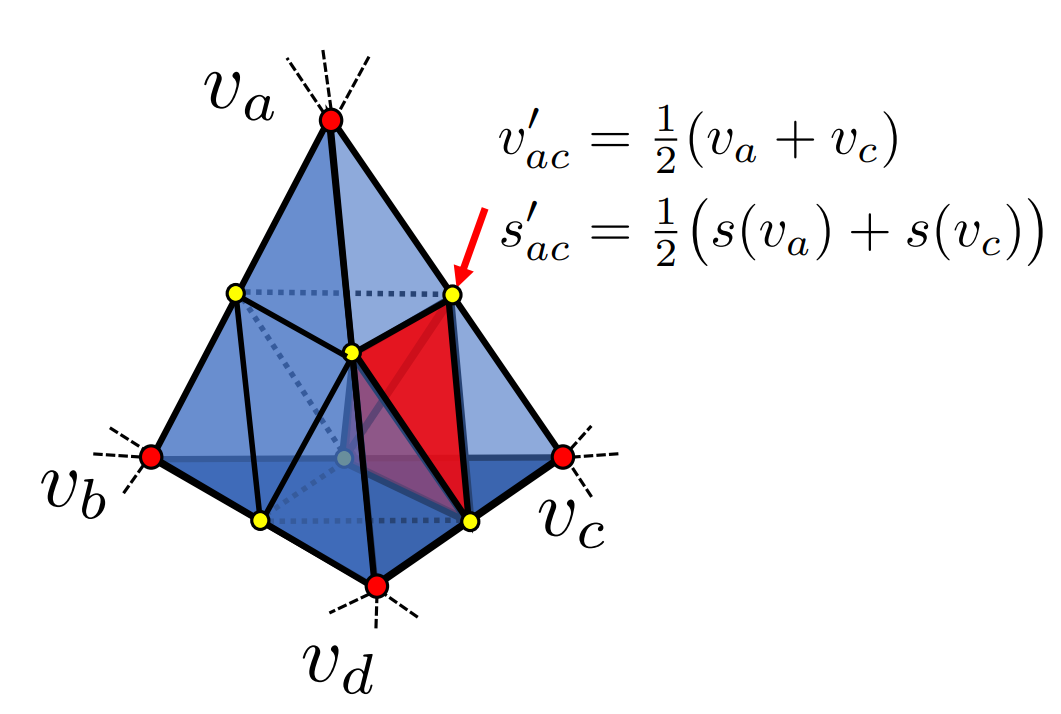
   Midpoints are added to each edge and the SDF values are interpolated. This increases the grid resolution in the regions of interest. After this step, unsubdivided tetrahedra would also be dropped.

Marching Tetrahedra

DMTet adopts the classic Marching Tetrahedra [4] algorithm to convert the vertices with SDF values, into a triangular mesh. The marching process consider 3 different cases, as depicted in the figure:

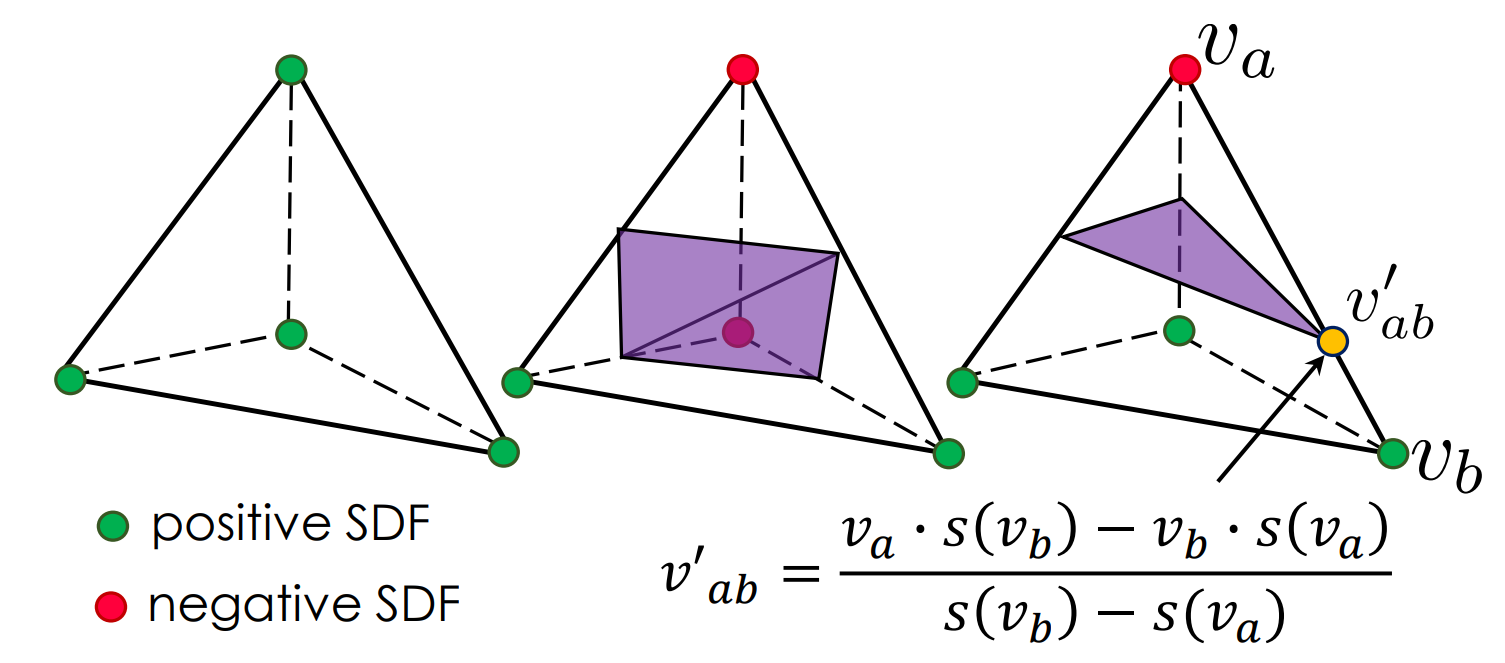
The signs could flip in all 3 cases and the surface would remain equivalent.

Learnable Surface Subdivision

An additional surface subdivision method is performed on the MT output mesh, following Loop Subdivision [5]. A new graph is built on the mesh, along with another GCN to predict the vertex offsets $v_i^{\prime}$ and the $\alpha_i$ weight for Loop Subdivision. The details of Loop Subdivision could also be found on this zhihu post.

Loss Functions

The optimization is what is tricky here. In different literatures using DMTet, the representation could be the similar, while the training objectives could be flexible. In the original DMTet, a 3D discriminator is used to construct an adversarial loss, along with a surface alignment loss and a regularization loss.

Surface Alignment loss Sample a set of points $P_{g t}$ from the surface of the ground truth mesh $M_{g t}$. Also sample a set of points from $M_{p r e d}$ to obtain $P_{\text {pred }}$, and minimize the L2 Chamfer Distance and the normal consistency loss between $P_{g t}$ and $P_{\text {pred }}$ :

\[L_{\mathrm{cd}}=\sum_{p \in P_{\text {pred }}} \min _{q \in P_{g t}}\|p-q\|_2+\sum_{q \in P_{g t}} \min _{p \in P_{p r e d}}\|q-p\|_2, L_{\text {normal }}=\sum_{p \in P_{\text {pred }}}\left(1-\left|\overrightarrow{\mathbf{n}}_p \cdot \overrightarrow{\mathbf{n}}_{\hat{q}}\right|\right),\]

where $\hat{q}$ is the point that corresponds to $p$ when computing the Chamfer Distance, and $\overrightarrow{\mathbf{n}}_{x}$ denotes the normal direction at point $p, \hat{q}$.

Adversarial Loss Similar to the adversarial loss proposed in LSGAN:

\[L_{\mathrm{D}}=\frac{1}{2}\left[\left(D\left(M_{g t}\right)-1\right)^2+D\left(M_{\text {pred }}\right)^2\right], L_{\mathrm{G}}=\frac{1}{2}\left[\left(D\left(M_{p r e d}\right)-1\right)^2\right]\]

Regularizations Directly using the GT SDF values as supervision:

\[L_{\mathrm{SDF}}=\sum_{v_i \in V_T}\left|s\left(v_i\right)-S D F\left(v_i, M_{g t}\right)\right|^2\]

where $S D F\left(v_i, M_{g t}\right)$ denotes the SDF value of point $v_i$ to the mesh $M_{g t}$.

And another $L_2$ regularization loss on the predicted vertex deformations:

\[L_{\text {def }}=\sum_{v_i \in V_T}\left\|\Delta v_i\right\|_2\]

The representation and SDF values are tuned on these loss functions iteratively.

Takeaway

Supervisions

Unlike NeRF-based representations, DMTet has a more explicit geometry that aligns with traditional 3D mesh representations. However, as a case-specific representation, the supervision is something thats worth considering. Relying solely on 3D discriminators is far from ideal. Recent works have been trying to add 2D discriminators with text or other conditions as another kind of supervision signal, to enhance the supervision.

Initialization

The initialization is highly unstable when we are depending on a point cloud feature extractor that are not case specific at all. Even in the official demo from Kaolin, the initial SDF values are loaded from pre-computed assets.

References

[1] Shen, T., Gao, J., Yin, K., Liu, M. Y., & Fidler, S. (2021). Deep marching tetrahedra: a hybrid representation for high-resolution 3d shape synthesis. Advances in Neural Information Processing Systems, 34, 6087-6101.

[2] Gao, J., Shen, T., Wang, Z., Chen, W., Yin, K., Li, D., … & Fidler, S. (2022). Get3d: A generative model of high quality 3d textured shapes learned from images. Advances In Neural Information Processing Systems, 35, 31841-31854.

[3] Liu, Z., Feng, Y., Black, M. J., Nowrouzezahrai, D., Paull, L., & Liu, W. (2023). MeshDiffusion: Score-based Generative 3D Mesh Modeling. arXiv preprint arXiv:2303.08133.

[4] Doi, A., & Koide, A. (1991). An efficient method of triangulating equi-valued surfaces by using tetrahedral cells. IEICE TRANSACTIONS on Information and Systems, 74(1), 214-224.

[5] Loop, C. (1987). Smooth subdivision surfaces based on triangles.

[6] DMTet Tutorial on Kaolin’s Github Repo.

Share: Twitter, QQ, Copy link